|
มัธยฐาน
มัธยฐาน คือ ค่าที่มีตำแหน่งอยู่กึ่งกลางของข้อมูลทั้งหมด เมื่อเรียบเรียงข้อมูลจากต่าน้อยที่สุดไปหาค่าที่
มากที่สุด หรือจากค่าที่มากที่สุดไปหาค่าที่น้อยที่สุด เราอาจใช้ตัวย่อ "Med" แทนค่ามัธยฐานของข้อมูล
ค่ามัธยฐานอาจเป็ฯค่าใดค่าหนึ่งของข้อมูล หรืออาจเป็ฯค่าที่คำนวณขึ้นมาใหม่ ซึ่งไม่ตรงกับค่าของข้อมูล
ใดๆก็ได้ ค่ามัธยฐานนิยมใช้กับข้อมูล ซึ่งสูงกว่าหรือต่ำกว่าค่าอื่นมากๆ
1. การหาค่ามัธยฐานของข้อมูลที่ไม่แจกความถี่ เมื่อจัดเรียงข้อมูลชุดหนึ่งซึ่งมี N ค่า ตำแหน่งของมัธยฐาน
จะคำนวณได้จากสูตร
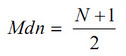Mdn คือ ค่ามัธยฐาน
N คือ ข้อมูลทั้งหมด
ตัวอย่างที่ 1 จงหามัธยฐานของข้อมูลดังนี้ 5, 8, 3, 20, 100, 6
วิธีคิด เรียงข้อมูลจากน้อยไปมากได้ดังนี้ 3 5 6 8 20 100
ตำแหน่งของค่ามัธยฐาน คือ = (6+1)/2 = 3.5
ดังนั้น ค่ามัธยฐาน คือ = (6+8)/2 = 7
2. การหาค่ามัธยฐานของข้อมูลที่แจกแจงความถี่แล้ว ซึ่งสามารถหาค่ามัธยฐานได้จากสูตร เมื่อจัดเรียง
ข้อมูลชุดหนึ่งซึ่งมี N ค่า ตำแหน่งของมัธยฐาน จะคำนวณได้จากสูตร
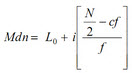Mdn คือ ค่ามัธยฐาน
Lo คือ ขอบเขตล่างของชั้นที่มีมัธยฐานอยู่
i คือ อันตรภาคชั้น (ช่วงห่างของข้อมูลแต่ละชั้น)
N คือ จำนวนข้อมูลทั้งหมด
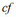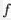 คือ ความถี่สะสมที่อยู่ก่อนถึงชั้นที่มีตำแหน่งมัธยฐาน
 คือ ความถี่ของคะแนนในชั้นที่มีมัธยฐาน
ตัวอย่างที่ 2 จงหามัธยฐานของข้อมูลที่แจกแจงความถี่ ดังตาราง
ความสูง (ซม.) |
จำนวน (คน) |
ความถี่สะสม |
143-147 |
2 |
2 |
148-152 |
5 |
7 |
153-157 |
7 |
14 |
158-162 |
11 |
25 |
*163-167 |
7 |
32 |
168-172 |
5 |
37 |
173-177 |
3 |
40 |
วิธีคิด ตำแหน่งของค่ามัธยฐาน = N/2 = 40/2 = 20
L = (157+198)/2 = 157.5
แทนค่าในสูตร Med = 157.5 + [(20-14)/11]5
≈ 160.23
ดังนั้น ค่ามัธยฐานของความสูง คือ ≈ 160.23
ที่มา : http://sathiti.blogspot.com/2013/02/blog-post_1236.html
|
