กฎแรงดึงดูดระหว่างมวลของนิวตัน
นักดาราศาสตร์และนักวิทยาศาสตร์ในสมัยโบราณสังเกตพบว่า ดวงจันทร์โคจรรอบโลกส่วนโลกและดาวเคราะห์ต่างๆ โคจรรอบดวงอาทิตย์ โดยวงโคจรของดวงจันทร์หรือดาวเคราะห์มีลักษณะเป็นวงกลมหรือวงรี แม้แคปเลอร์ (Kepler) จะพบกฎการโคจรของดาวเคราะห์รอบดวงอาทิตย์ได้ แต่ก็ยังไม่มีใครสามารถอธิบายเหตุผลในการโคจรลักษณะเช่นนี้ได้ จนกระทั่งนิวตันได้นำผลการสังเกตของนักดาราศาสตร์ทั้งหลายมาสรุปว่า การที่ดาวเคราะห์โคจรรอบดวงอาทิตย์ได้ เนื่องจากมีแรงกระทำระหว่างดวงอาทิตย์กับดาวเคราะห์ เขาเชื่อว่าแรงนี้เป็นแรงดึงดูดระหว่างมวลของดวงอาทิตย์กับมวลของดาวเคราะห ์และยังเชื่อต่อไปว่าแรงดึงดูดระหว่างมวลเป็นแรงธรรมชาติ และจะมีแรงดึงดูดระหว่างวัตถุทุกชนิดที่มีมวลในเอกภพ นิวตันจึงเสนอกฎแรงดึงดูดระหว่างมวลซึ่งมีใจความว่า "วัตถุทั้งหลายในเอกภพจะออกแรงดึงดูดซึ่งกันและกัน โดยขนาดของแรงดึงดูดระหว่างวัตถุคู้หนึ่งๆ จะแปรผันตรงกับผลคูณระหว่างมวลวัตถุทั้งสองและจะแปรผกผันกับกำลังสองระยะทางระหว่างวัตถุทั้งสองนั้น"
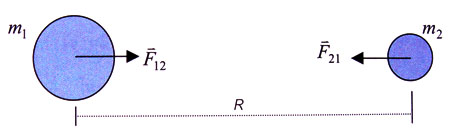
ถ้า m1 และเป็น m2 มวลของวัตถุทั้งสองซึ่งอยู่ห่างกันเป็นระยะทาง R ขนาดของแรงดึงดูดระหว่างมวล fgเป็น
ขนาดของทั้ง 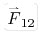 และ และ 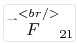 ตามกฎแรงดึงดูดระหว่างมวลของนิวตัน จะเป็นไปตามสมการ ตามกฎแรงดึงดูดระหว่างมวลของนิวตัน จะเป็นไปตามสมการ
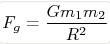
G เป็นค่าคงตัวของแรงดึงดูดระหว่างมวล และเป็นค่าเดียวกันเสมอ ไม่มีวัตถุที่ดึงดูดกันจะเป็นวัตถุใดๆ ก็ตาม G นี้เรียกว่า ค่าคงตัวความโน้มถ่วงสากล (universal gravitational constant) กฎแรงดึงดูดระหว่างมวลของนิวตันตามสมการ (1) นี้ช่วยให้สามารถคำนวณหาแรงดึงดูดระหว่าง
วัตถุคู่หนึ่งๆได้ เมื่อทราบค่าคงตัว G เนื่องจาก G มีค่าเท่ากับ 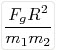 ในทางปฏิบัติการหาค่า G นั้น ค่ามวล m1และ m2 าได้ด้วยการชั่ง ส่วนระยะทางระหว่างมวลทั้งสอง R ก็สามารถวัดได้ ในกรณีที่วัตถุมีขนาดใหญ่เหมือนรูปทรงกลม ระยะ R คือระยะทางระหว่างศูนย์กลางของทรงกลมทั้งสอง แต่มวลที่ใช้ในห้องปฏิบัติการโดยทั่วไปแล้วจะทำให้เกิดแรงดึงดูดน้อยมาก การวัดขนาดแรงดึงดูด fg จึงทำได้ยากมาก แต่เฮนรีคาเวนดิช (Henry Cavendish) นักวิทยาศาสตร์ชาวอังกฤษสามารถคิดวิธีวัดแรงดึงดูดค่าน้อยๆ นี้ได้ โดยใช้เครื่องชั่งแบบแรงบิด (torsion balance) และสามารถหาค่าของ G ได้ (ประมาณ 100 ปี หลังจากนิวตันได้ตั้งกฎนี้ขึ้น)การทดลองวัดค่าแรงดึงดูดระหว่างมวลของคาเวนดิช ในทางปฏิบัติการหาค่า G นั้น ค่ามวล m1และ m2 าได้ด้วยการชั่ง ส่วนระยะทางระหว่างมวลทั้งสอง R ก็สามารถวัดได้ ในกรณีที่วัตถุมีขนาดใหญ่เหมือนรูปทรงกลม ระยะ R คือระยะทางระหว่างศูนย์กลางของทรงกลมทั้งสอง แต่มวลที่ใช้ในห้องปฏิบัติการโดยทั่วไปแล้วจะทำให้เกิดแรงดึงดูดน้อยมาก การวัดขนาดแรงดึงดูด fg จึงทำได้ยากมาก แต่เฮนรีคาเวนดิช (Henry Cavendish) นักวิทยาศาสตร์ชาวอังกฤษสามารถคิดวิธีวัดแรงดึงดูดค่าน้อยๆ นี้ได้ โดยใช้เครื่องชั่งแบบแรงบิด (torsion balance) และสามารถหาค่าของ G ได้ (ประมาณ 100 ปี หลังจากนิวตันได้ตั้งกฎนี้ขึ้น)การทดลองวัดค่าแรงดึงดูดระหว่างมวลของคาเวนดิช
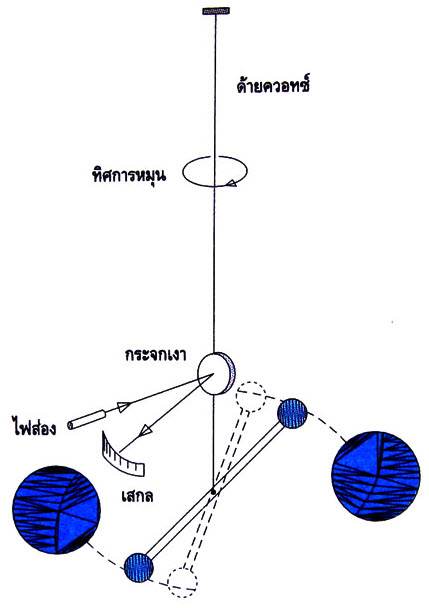
เฮนรี คาเวนดิช นักวิทยาศาสตร์ชาวอังกฤษสามารถคิดวิธีวัดแรงดึงดูดค่าน้อยๆ นี้โดยใช้คานเบา ยาวประมาณ 2 เมตรและมีลูกกลมเล็กๆ ทำด้วยตะกั่ว ติดที่ปลายคานด้านละลูก ดังรูป คานนี้ถูกแขวนด้วยสายควอทซ์เส้นเล็กๆ คาเวนดิชทดลองหามาก่อนแล้วว่า ต้องใช้แรงเท่าใด ในการทำให้คานและสายควอทซ์บิดไปเป็นมุมต่างๆ เมื่อคาเวนดิชนำลูกกลมใหญ่ทำด้วยตะกั่วมาใกล้ลูกกลมเล็กที่ปลายคานข้างละลูก โดยให้ห่างจากลูกกลมเล็กเท่ากันสายควอทซ์จะบิดและลูกกลมเล็กจะเบี่ยงเบนไปอยู่ในตำแหน่งสมดุลใหม่ จากการวัดมุมที่สายควอทซ์บิดไป คาเวนดิชคำนวณหาแรงดึงดูดระหว่างลูกกลมเล็กและลูกกลมใหญ่ได้ เมื่อวัดมวลของลูกกลม และระยะทางระหว่างลูกกลมแล้ว คาเวนดิช สามารถหาค่าคงตัวความโน้มถ่วงสากล G ได้ ตามระบบ
เอสไอค่าGที่เป็นที่ยอมรับปัจจุบันมีค่า 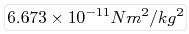
จากตัวอย่างดังกล่าวจะเห็นว่า แรงโลกดึงดูดดวงจันทร์มีค่ามาก ส่วนแรงดึงดูดระหว่างมวลต่างๆ ที่เราพบเห็นในชีวิตประจำวันมีค่าน้อยมาก นอกจากนี้ยังพบ แรงดึงดูดระหว่างมวลของโลกกับมวลของวัตถุ คือ น้ำหนักวัตถุนั่นเอง ในการหามวลของวัตถุต่างๆ บนโลกเราอาจหาได้โดยใช้เครื่องชั่ง แต่กรณีที่วัตถุมีขนาดใหญ่มาก เช่น โลก ดวงจันทร์ ดวงอาทิตย์ ดาวเคราะห์ต่างๆ เราไม่สามารถใช้เครื่องชั่งชั่งมวลที่มีขนาดใหญ่เช่นนั้นได้ แต่เราสามารถใช้กฎแรงดึงดูดระหว่างมวลของนิวตัน คำนวณหามวลของวัตถุขนาดใหญ่ๆ เช่น โลก และดวงดาวได้ กฎแรงดึงดูดระหว่างมวลทำให้สามารถเข้าใจสมบัติและลักษณะการเคลื่อนที่ของดาวเคราะห์ ดวงจันทร์ ได้เป็นอย่างดี อาจพิสูจน์ได้ว่าแรงที่เป็นปฏิภาคกับ 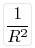 ทำให้วงโคจรโดยทั่วไปจะเป็นวงรี(ellipse) วงกลมอาจถือว่าเป็นกรณีพิเศษของวงรี ทำให้วงโคจรโดยทั่วไปจะเป็นวงรี(ellipse) วงกลมอาจถือว่าเป็นกรณีพิเศษของวงรี


http://kobchai12.wordpress.com/2011/11/28/กฎแรงดึงดูดระหว่างมวลข/
|
|
|

